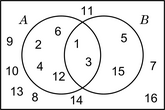
Intersección, Inclusión y Disyunción

Intersección

Dado que los conjuntos pueden tener elementos comunes, las regiones encerradas por sus líneas límite se superponen. El conjunto de los elementos que pertenecen simultáneamente a otros dos es la intersección de ambos.

A = {1; 2; 3; 4; 6; 12} B = {1; 3; 5; 15} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 15} U = {x | x es natural menor o igual que 16}

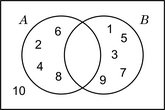
Inclusión

Si todos los elementos de un conjunto son parte de los elementos de otro, se dice que el primero es un subconjunto del segundo o que está incluido en el segundo. En los diagramas de Venn, todas las regiones de superposición posibles deben ser representadas. Y, cuando hay regiones que no contienen elementos, la situación se indica anulándolas (con un color de fondo distinto).

A = {1; 2; 3; 4; 6; 12} B = {1; 2; 3; 6} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 6} U = {x | x es natural menor o igual que 12}

Disyunción

Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.

A = {2; 4; 6; 8} B = {1; 3; 5; 7; 9} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
A = {x | x es par y de una cifra} B = {x | x es impar y de una cifra} U = {x | x es natural menor o igual que 10}

Operaciones con tres conjuntos - Reunión, Intersección,Diferencia y Complemento.

Diagrama de Venn

Saludos Lector :D