Gráficos para Estadística.

Histograma

Un histograma es una gráfica que puede utilizar para evaluar la forma y dispersión de datos de muestra continuos. Puede crear un histograma antes o durante un análisis para ayudar a confirmar supuestos y orientar análisis posteriores.  es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados, ya sea en forma diferencial o acumulada. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o la muestra, respecto a una característica, cuantitativa y continua, de la misma y que es de interés para el observador.

Gráfico de Barras.

Una gráfica de barras es una gráfica que usted puede utilizar para comparar las alturas de barras de medidas de categorías. Las gráficas de barras pueden constar de cuentas por categoría, de estadísticas diferentes por categorías o de valores de resumen. La altura de las barras representa la magnitud de los valores. Por ejemplo, las barras podrían representar:

• Las ventas totales de cuatro tiendas sucursales durante un año
• La media de los diámetros de piezas producidas por cuatro máquinas diferentes en una fábrica durante una semana
• Los conteos de visitantes a cuatro destinos turísticos locales durante un fin de semana

Es una forma de representar gráficamente un conjunto de datos o valores, y está conformado por barras rectangulares de longitudes proporcionales a los valores representados. Los gráficos de barras son usados para comparar dos o más valores. Las barras pueden orientarse verticalmente u horizontalmente.

Gráfica de Pastel.

Es un recurso estadístico que se utiliza para representar porcentajes y proporciones. El número de elementos comparados dentro de una gráfica circular suele ser de más de cuatro.

Al igual que en la gráfica de barras, el empleo de tonalidades o colores facilita la diferenciación de los porcentajes o proporciones. A diferencia de otros tipos de gráficos, el circular no tiene ejes x o y.

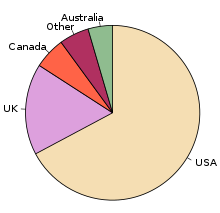
Gráfico de dispersión.

Una gráfica de dispersión puede ser usada para datos en la forma de parejas ordenadas de números. El resultado será un montón de puntos "dispersos" alrededor del plano.

Si la tendencia general es que los puntos suban a la derecha de la gráfica, entonces decimos que hay una correlación positiva entre las dos variables medidas. Si los puntos caen a la izquierda de la gráfica, decimos que hay una correlación negativa. Si no hay tendencia general, entonces no hay correlación.

Si la tendencia no es muy pronunciada – esto es, los puntos están dispersos ampliamente – entonces decimos que las variables están débilmente correlacionadas. Si la correlación es más pronunciada, decimos que las variables están fuertemente correlacionadas.

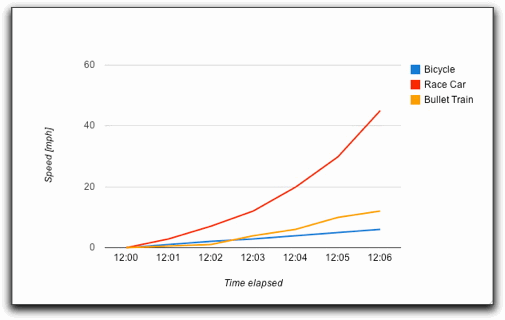
Gráfica de Línea.

Los gráficos de líneas son perfectos para mostrar tendencias a lo largo de un período de tiempo.

Los gráficos de líneas son una buena solución para representar datos numéricos de manera visual. Resultan especialmente útiles para expresar los cambios que se producen en los valores entre las distintas categorías de datos.

Gráficos de columnas tridimensionales

Los tipos de diagramas 3D resultan muy atractivos por el efecto tridimensional de profundidad. Ofrecen las mismas variantes que los diagramas 2D más una variante nueva que da más profundidad al diagrama, resultando un total de 16 variantes.

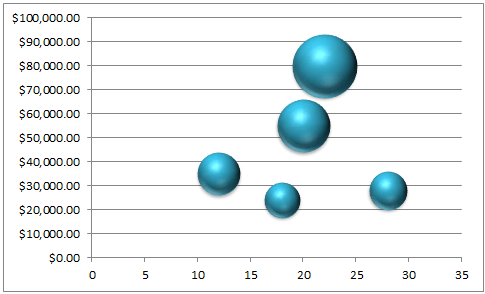
Gráfico de burbujas.

Los gráficos de burbuja nos permiten mostrar tres dimensiones de datos en un gráfico de dos dimensiones. El gráfico de burbuja es una variación del gráfico de dispersión en donde los puntos son reemplazados por burbujas.

El tamaño de las burbujas es lo que representa la tercera dimensión de datos en el gráfico. Las burbujas se grafican de acuerdo a los valores de "X" y de "Y" mientras que su tamaño será proporcional al tercer valor. Los gráficos de burbuja son frecuentemente utilizados para presentar información financiera ya que los diferentes tamaños de las burbujas enfatizan adecuadamente los diferentes valores financieros.

Saludos Lector! :D

Intersección, Inclusión y Disyunción

Intersección

Dado que los conjuntos pueden tener elementos comunes, las regiones encerradas por sus líneas límite se superponen. El conjunto de los elementos que pertenecen simultáneamente a otros dos es la intersección de ambos.

A = {1; 2; 3; 4; 6; 12} B = {1; 3; 5; 15} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 15} U = {x | x es natural menor o igual que 16}

Inclusión

Si todos los elementos de un conjunto son parte de los elementos de otro, se dice que el primero es un subconjunto del segundo o que está incluido en el segundo. En los diagramas de Venn, todas las regiones de superposición posibles deben ser representadas. Y, cuando hay regiones que no contienen elementos, la situación se indica anulándolas (con un color de fondo distinto).

A = {1; 2; 3; 4; 6; 12} B = {1; 2; 3; 6} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12}
A = {x | x es divisor natural de 12} B = {x | x es divisor natural de 6} U = {x | x es natural menor o igual que 12}

Disyunción

Cuando los conjuntos no tienen elementos comunes, la región de superposición queda vacía.

A = {2; 4; 6; 8} B = {1; 3; 5; 7; 9} U = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
A = {x | x es par y de una cifra} B = {x | x es impar y de una cifra} U = {x | x es natural menor o igual que 10}

Operaciones con tres conjuntos - Reunión, Intersección,Diferencia y Complemento.

Diagrama de Venn

Saludos Lector :D

Vectores

Vectores

Un vector fijo  es un segmento orientado que va del punto A (origen) al punto B (extremo).

Un vector fijo es nulo cuando el origen y su extremo coinciden.

Módulo del vector 

Es la longitud del segmento AB, se representa por .

Dirección del vector 

Es la dirección de la recta que contiene al vector o de cualquier recta paralela a ella.

Sentido del vector 

El que va del origen A al extremo B.

Vectores equipolentes

Dos vectores son equipolentes cuando tienen igual módulo, dirección y sentido.

Vector libre

El conjunto de todos los vectores equipolentes entre sí se llama vector libre. Cada vector fijo es un representante del vector libre.

Vector de posición de un punto en el plano de coordenadas

El vector  que une el origen de coordenadas O con un punto P se llama vector de posición del punto P.

Coordenadas de un vector en el plano

Si las coordenadas de A y B son:

Las coordenadas o componentes del vector  son las coordenadas del extremo menos las coordenadas del origen.

Módulo de un vector

Si las coordenadas de A y B son:

Las coordenadas o componentes del vector  son las coordenadas del extremo menos las coordenadas del origen.

Si tenemos las componentes de un vector:

Distancia entre dos puntos

La distancia entre dos puntos es igual al módulo del vector que tiene de extremos dichos puntos.

Vector unitario

Los vectores unitarios tienen de módulo la unidad.

Suma de vectores

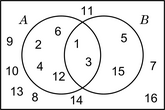
Para sumar dos vectores libres  y  se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Regla del paralelogramo 

Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.

Para sumar dos vectores se suman sus respectivas componentes.

Resta de vectores

Para restar dos vectores libres  y  se suma  con el opuesto de . Las componentes del vector resta se obtienen restando las componentes de los vectores.

Producto de un número por un vector

El producto de un número k por un vector  es otro vector:

• De igual dirección que el vector .
• Del mismo sentido que el vector  si k es positivo.
• De sentido contrario del vector  si k es negativo.
• De módulo 

Las componentes del vector resultante se obtienen multiplicando por K las componentes del vector.

Coordenadas del punto medio de un segmento

Las coordenadas del punto medio de un segmento son la semisuma de las coordenadas de los extremos.

Condición para qué tres puntos estén alineados

Los puntos A (x₁, y₁), B(x₂, y₂) y C(x₃, y₃) están alineados siempre que los vectores  tengan la misma dirección. Esto ocurre cuando sus coordenadas son proporcionales.

Simétrico de un punto respecto de otro

Si A' es el simétrico de A respecto de M, entonces M es el punto medio del segmento AA'. Por lo que se verificará igualdad:

Coordenadas del baricentro

Baricentro o centro de gravedad de un triángulo es el punto de intersección de sus medianas.

Las coordenadas del baricentro son:

División de un segmento en una relación dada

Dividir un segmento AB en una relación dada r es determinar un punto P de la recta que contiene al segmento AB, de modo que las dos partes, PA y PB, están en la relación r:

                                        

División de un segmento en una relación dada

Dividir un segmento AB en una relación dada r es determinar un punto P de la recta que contiene al segmento AB, de modo que las dos partes, PA y PB, están en la relación r

LINKS PARA VER TUTORIALES SOBRE ÉSTE TEMA EN YOUTUBE:

 

Suma y Resta de Vector

Módulo de Vector

Saludos Lector! :D